MATEMÁTICAS
La «ciencia matemática» practicada por Pitágoras y los matematikoi difiere del tratamiento de esta ciencia que se lleva a cabo en universidades o instituciones modernas. Los pitagóricos no estaban interesados en «formular o resolver problemas matemáticos», ni existían para ellos «problemas abiertos» en el sentido tradicional del término. El interés de Pitágoras era el de «los principios» de la matemática, «el concepto de número», «el concepto de triángulo» (u otras figuras geométricas) y la idea abstracta de «prueba». Como señala Brumbaug, "Es difícil para nosotros hoy en día, acostumbrados como estamos a la abstracción pura de las matemáticas y el acto mental de la generalización, el apreciar la originalidad de la contribución pitagórica."
Pitágoras reconocía en los números propiedades tales como «personalidad», «masculinos y femeninos», «perfectos o imperfectos», «bellos y feos». El número diez era especialmente valorado, por ser la suma de los primeros cuatro enteros [1 + 2 + 3 + 4 = 10], los cuales se pueden disponer en forma de triángulo perfecto: la «tetraktys». Para los pitagóricos, «las cosas son números», y observaban esta relación en el cosmos, la astronomía o la música.
Entre los descubrimientos matemáticos que se atribuyen a la escuela de Pitágoras se encuentran:
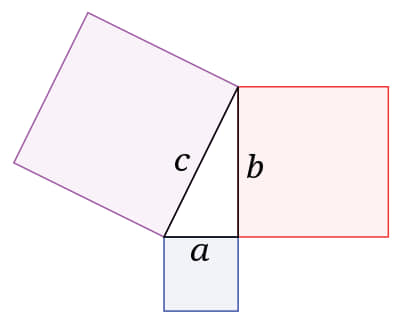
Teorema de Pitágoras
El teorema de Pitágoras. En un triángulo rectángulo: «la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa». Si bien este resultado y las ternas pitagóricas eran conceptos ya conocidos y utilizados por los matemáticos babilonios y de la India desde mucho tiempo, fueron los pitagóricos los primeros que enunciaron una demostración formal del teorema; esta demostración es la que se encuentra en Los Elementos de Euclides. También demostraron el inverso del teorema: si los lados de un triángulo satisfacen la ecuación, entonces el triángulo es rectángulo. Debe hacerse hincapié además, en que «el cuadrado de un número» no era interpretado como «un número multiplicado por sí mismo», como se concibe actualmente, sino en términos de los lados de un «cuadrado geométrico».
Dodecaedro
Sólidos perfectos.
Los pitagóricos demostraron que sólo existen 5 poliedros regulares. Se cree que Pitágoras sabía cómo construir los tres (o cuatro) primeros, pero fue Hipaso de Metaponto (470 a. C.) quien descubrió el dodecaedro. Se debe a Teeteto la demostración de que no existen otros poliedros regulares convexos.
Ángulos interiores de un triángulo.
Encontraron que la suma de los ángulos interiores de un triángulo es igual a dos rectos, así como la generalización de este resultado a polígonos de n - lados.
Un triángulo inscrito en un semicírculo es un triángulo rectángulo. Proposición de origen pitagórico (según Diógenes).
Construcción de figuras dada un área determinada. Por ejemplo la resolución de ecuaciones como a•(a-x)=x² por métodos geométricos.
La irracionalidad de la raíz cuadrada de 2. Los pitagóricos descubrieron que la diagonal de un cuadrado de lado 1 no puede expresarse como un cociente de números enteros. Este evento marca el descubrimiento de los números irracionales, si bien a la época, sólo podía entenderse en términos de inconmensurabilidad de magnitudes [números] «enteras», o «proporciones geométricas». Un método de aproximación (aproximación diofántica) posiblememente desarrollado por Arquitas, utiliza el algoritmo de Euclides, y está presente en Los Elementos.
El descubrimiento de los Números perfectos y los Números amigos
Jámblico atribuye a Pitágoras el haber descubierto el par de números amigos (220, 284).
Medias
Los pitagóricos examinaron exhaustivamente las razones y proporciones entre los números enteros; la media aritmética, la media geométrica y la media armónica y las relaciones entre ellas.
El descubrimiento de los Números poligonales
Un número es «poligonal» (triangular, cuadrangular, pentagonal, hexagonal, etc.) si tal número de puntos se pueden acomodar formando el polígono correspondiente (ver figura).
Tetraktys. Se atribuye a Pitágoras el haber ideado la «Tetraktys», la figura triangular compuesta por diez puntos ordenados en cuatro filas. Fue un símbolo de especial importancia para los pitagóricos, que solían juramentar en su nombre.
INFLUENCIA
Los testimonios pre-aristotélicos dan cuenta de la gran fama que Pitágoras alcanzó en vida. La imagen moderna es la de un maestro en matemáticas, «el primer matemático puro» (dada la fuerte conexión con el «teorema de Pitágoras» de la geometría euclidiana), conocedor de ciencias tales como la astronomía o la cosmología. Si bien fue uno de los pensadores más conocidos de su época, el elemento religioso parece haber sido el predominante en su carácter, y su doctrina mística la que más influenció a sus contemporáneos.
Pitágoras pasa por ser un experto en temas como la inmortalidad, la reencarnación del alma y su destino después de la muerte, ritos y rituales religiosos y de auto-control y disciplina. Tanto Platón como Aristóteles coinciden no sólo en resaltar su influencia, sino también en situarlo como “fundador de un modo de vida”. En particular, Aristóteles solamente menciona a «los así llamados pitagóricos» para referirse al pitagorismo del siglo V, y no parece atribuirle una continuidad filosófica iniciada en Tales. Platón hace referencia al “fundador de un modo de vida” y no hace alusión a él cuando escribe sobre la historia de la filosofía. Para ambos, Pitágoras no es parte de la tradición cosmológica y metafísica presocrática.
Las instituciones pitagóricas no intentaban sustraer al individuo de sus actividades sociales o políticas, dedicándose a la contemplación religiosa o filosófica exclusivamente, más bien proclamaban la calma y un elevado tono de carácter; para los pitagóricos «la vida debía exhibir tanto en lo personal como en lo social, una reflexión sobre el orden y la armonía del universo».
Después de la disolución de la escuela de Crotona, los pitagóricos se esparcieron por otras partes de Grecia. Para los tiempos de Sócrates, ya hay evidencia certera de Filolao, Lisis, Clinias, Éurito y Arquitas. Estos filósofos pitagóricos, entre otros representantes de la tradición helenística eran muy distintos a los primeros pitagóricos (del tiempo de Cicerón), caracterizados por un gran apego a la figura del maestro. Este neopitagorismo se fue sumergiendo paulatinamente dentro del misticismo familiar de los neoplatónicos. La tradición que asocia la metafísica platónica a Pitágoras parece existir ya desde el siglo IV a.C., entre los propios discípulos de Platón. La clara distinción que hace Aristóteles entre ambos y que está acorde con el desarrollo general de la filosofía griega, termina por decantarse en favor de una tardía tradición neopitagórica que se identifica con un platonismo maduro.
________________________________________________
Fin de la Tercera y Última Parte (17C)
Fuentes: Wikipedia, Afm Elierf







No hay comentarios:
Publicar un comentario